 |
ПОЛИГРАФ - ФОРУМ
Для общения по теме " Детекция лжи "
|
| Предыдущая тема :: Следующая тема |
| Автор |
Сообщение |
$erP
Site Admin
Зарегистрирован: 29.06.2005
Сообщения: 7880
Откуда: Москва
|
 Добавлено: Ср Мар 29, 2023 2:30 pm Заголовок сообщения: Формула Ликкена Добавлено: Ср Мар 29, 2023 2:30 pm Заголовок сообщения: Формула Ликкена |
 |
|
Тема навеяна из сравнительного разбора тестов формата "ряды"...
Полагаю, что зашедшее в этой теме обсуждение "формулы Ликкена" - это совсем отдельный вопрос, который следует выделить в самостоятельную тему... что, собственно, и сделал...
Предварительно: я не связан ни с кем никакими моральными или коммерческими обязательствами, мне никто не доверял эту страшную тайну, взяв с меня не менее страшную клятву о неразглашении или дав мне за молчание кучу денег... Поэтому я могу себе позволить описать свой собственный алгоритм решения задачи под названием "утерянная формула Ликкена"… а все совпадения с шагами тех, кто проделал этот путь до меня... самостоятельно или с чьей-то помощью... совершенно случайны... или не случайны... Бог его знает...
Мне для расшифровки "формулы Ликкена" понадобилась книга Виленкина "Комбинаторика", желательно 2015, а не 1968 года издания, неделя времени на её изучение, осмысление и применение изученного к имеющимся данным... Руки дошли до писанины только сейчас...
"Формула Ликкена" – это, скорее, алгоритм, описывающий последовательное использование разных формул на разных этапах обработки получения данных. Наверняка можно все расчёты впихнуть в итоге одну формулу… но вряд ли сам Ликкен делал так… поскольку редкая мозговая крыша не съедет от такого нагромождения…
Возьмемся с помощью комбинаторики получить те данные, которые представлены в исходной таблице Ликкена.
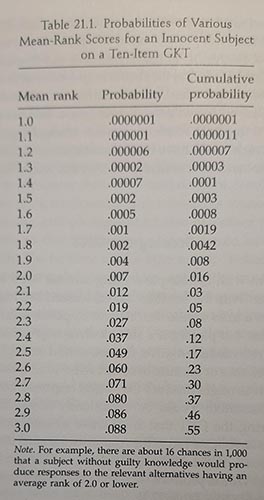
Данные в таблице представлены для следующих условий: в тесте пять ранжируемых вопросов (1R и 4 C); для ранжирования используются ранги от 1 – самая большая реакция до 5 – самая маленькая реакция; тест повторен 10 раз; после 10 повторов образуется ряд из 10ти рангов (каждый ранг от 1 до 5) на релевантные вопросы.
Например: 3; 2; 5; 4; 2; 2; 4; 4; 1; 3
Суммарный (он же средний суммарный) ранг на релевантный вопрос складывается из суммы рангов в последовательности. В данном случае суммарный ранг 3 + 2 + 5 + 4 + 2 + 2 + 4 + 4 + 1 + 3 = 30. Средний ранг 30/10 = 3.
Предварительно следует понимать, что суммарный ранг 30 (=средний ранг 3) можно получить не одной единственной комбинацией (последовательностью) рангов, а каким-то различным по количеству множеством таких комбинаций. Например, суммарный ранг 30, помимо представленной выше последовательности рангов, можно получить и такой последовательностью рангов на релевантный вопросы: 5; 5; 5; 5; 2; 2; 2; 2; 1; 1. Почему бы и нет? Теоретически такое возможно, и не учитывать такую возможность нельзя.
По таблице Ликкена, вероятность получения суммарного ранга 30 (=среднего ранга 3) составляет 0,088. Чтобы рассчитать это значение, необходимо
1) вычислить вероятность выпадания одной единственной комбинации с любым суммарным рангом (=средним рангом).
2) вычислить общее количество комбинаций рангов, которыми можно получить этот суммарный ранг 30 (=средний 3), и
3) полученное значение общего количество комбинаций получения суммарного ранга 30 (=среднего ранга 3) умножить на вероятность выпадания одной единственной комбинации.
Собственно, пункты 1 – 2 – 3 --- это и есть "формула Ликкена".
Пройдемся по пунктам данного алгоритма.
1) вычислить вероятность выпадания одной единственной комбинации
Очень легко. Как это делается.
Во первых, по бытовому, на пальцах…
Сначала издалека, с примера, который всем известен.
Если Вы бросаете кубик, то вероятность выпадания какого-то числа на грани куба составляет 1/6. Если Вы бросаете кубик 10 раз, то вероятность выпадания какой то комбинации из чисел, написанных на гранях куба, составляет 1/6 помножить на себя 10 раз.
В ранжировании вопросов теста имеем тот же процесс, только кубик состоит из пяти граней...
То есть если тест повторяется 1 раз, ранг от 1 до 5 достается релевантному вопросу с вероятностью 1/5. А если тест повторяется 10 раз, то вероятность получения релевантным вопросом ранга от 1 до 5ти составляет 1/5 помножить на себя 10 раз.
Если 1/5 помножить на себя 10 раз, то получится 0,0000001024.
0,0000001024 - это искомая вероятность выпадания одной комбинации.
Во-вторых, по умному, по Виленкину.
Ряду из 10 чисел, когда каждое число от 1 до 5ти появляется каждый раз с равной вероятностью, имеем т.н. процесс "размещение с повторениями", см. Виленкин, стр. 18, формула (1). По формуле (1) получаем, что количество комбинаций из 10 чисел по 5 составляет 5 в 10й степени = 9 765 625.
То есть, "выбирая" 10 раз одно число из ряда от 1 до 5ти 10 раз, получаем какую-то комбинацию из 10 чисел; и всё разнообразие этих комбинаций представлено в количестве 9 765 625.
Соответственно, вероятность выпадания одной комбинации составляет 1/ 9 765 625 = 0,0000001024.
2) Теперь надо посчитать количество таких последовательностей, в которых суммарный ранг составляет 30 (=средний ранг 3).
Это и есть самое сложное в "формуле Ликкена". Причём самое сложное не с точки зрения понимания, как это сделать, а точки зрения рутинной хлопотности расчётов. Не представляю, как Ликкен это считал всё вручную… сколько времени у него это заняло… Хотя… если он воспользовался тем приёмом, который использовал я, то… не так уж и много времени это заняло…
Принципиально как вычислить количество комбинаций из 10ти чисел от 1 до 5ти, так чтобы их сумма составила 30, можно изучить в учебнике Виленкина, гл. IV, "Разбиения", стр. 120. Полезно всё. Но чтобы понять, что написано в этой главе, надо понимать, что написано на предыдущих 120ти страницах.
Окончательная формула вычисления количества комбинаций дана на стр. 250.
Средствами форму её не переписать. Да и смысла нет. Чтобы получить значение по этой формуле, надо вычислить очень длинный многочлен, сложенный из умножающихся друг на друга факториалов.
Без компьютера точно с ума сойдёшь это всё считать.
И даже компьютер тут может оказаться мало полезным, поскольку забить в тот же Excel кучу формул перемножающихся факториалов – это та ещё морока…
Компьютер в этом деле является действительным помощником для тех, кто умеет составлять программы… причем хоть на самом древнем Бэйсике (кстати да… можно вспомнить-освежить... Excel же обрабатывает макросы на бейсике… )
Но... есть более простой и лёгкий вариант... Быстрые данные в полуручном режиме можно сделать, если заметить, что функция распределения количества комбинаций в зависимости от количества повторов теста представляет собой так называемый "m-мерный треугольник Паскаля", в котором значение в определенной позиции строки равно сумме значений с определенных позиций из предшествующей строки.
И вот эта закономерность в Excel реализуется "руками" буквально в 60 секунд.
Буква "m" означает, что в данном случае используется 5 значений от 1 до 5ти для присвоения ранга релевантному вопросу.
И тогда "треугольник Паскаля" выглядит следующим образом.
Тык: треугольник Паскаля целиком
Строки этого треугольника – количество предъявлений теста.
В каждой клеточке этой строки – искомое количество комбинаций для данного количества повторений, выдающих строго определенный суммарный ранг.
Если сложить все значения 10й строчки (это значения для 10ти повторений), то получится искомое 9 765 625 – всеобщее количество комбинаций рангов для 10ти повторений теста.
3) Далее получить вероятности выпадания той или иной комбинации с суммарным рангом 30 (=средний ранг 3) уже совсем просто: значение в клетке треугольника Паскаля из 10й строки умножается на вероятность выпадания одной комбинации (помним… 0,0000001024). В итоге имеем вероятности получения всех комбинаций, составляющих определенный суммарный ранг.
Не поленился, сделал это не только для 10ти, а для повторов от 2х до 15ти… интересно было глянуть на картину в целом… на всеобщую динамику показателей.
Тык: Таблица вероятностей для теста из 5ти ранжируемых вопросов, количество повторов теста от 2х до 15ти.
Для сравнения – сопоставил рядом расчётные данные таблицы для 10ти предъявлений с оригинальной таблицей Ликкена.
Тык: Сравнительные таблицы.
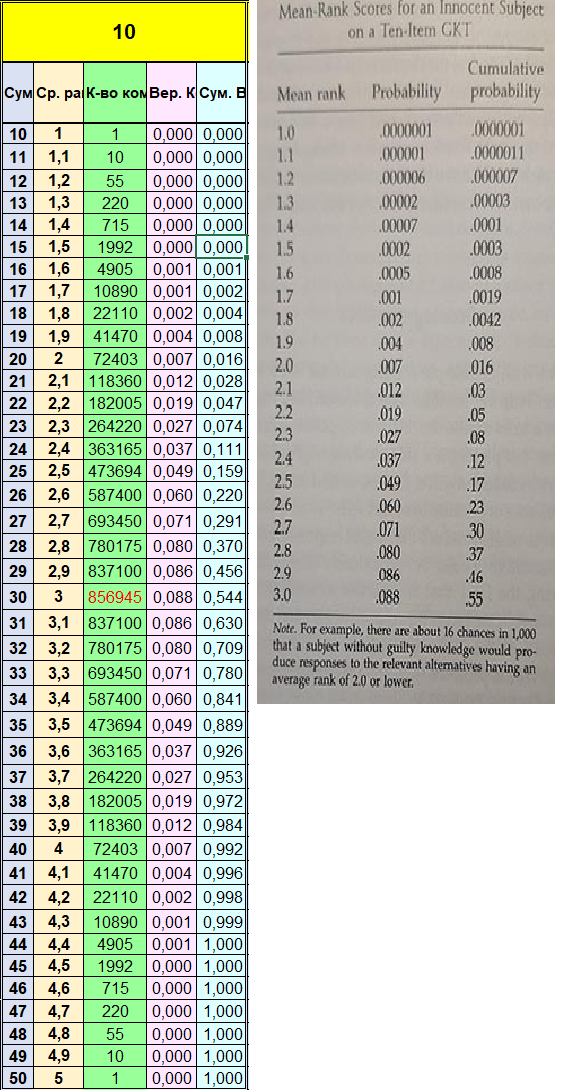
Таким же образом без проблем можно составить таблицы для наиболее часто встречаемых форматов тестов: с количеством ранжируемых вопросов от 4х до… ну, например, до 7ми… Но учитывая то, что большинство тестов состоит всё-таки из 5ти ранжируемых вопросов, наиболее востребованными в практическом плане были бы данные именно этой таблицы.
"Были бы" – не оборот речи… поскольку теперь точно понятно, что в практическом плане данные "формулы Ликкена" – это бесполезные для полиграфолога данные… не дающие то, что необходимо полиграфологу на самом деле…
Видимо, об этом надо будет сказать еще раз… поэтому... не переключайтесь…
_________________
Мое почтение... $erP
................................... ЛЕГКО СОЛГАТЬ ТЯЖЕЛО |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Ср Мар 29, 2023 8:34 pm Заголовок сообщения: Добавлено: Ср Мар 29, 2023 8:34 pm Заголовок сообщения: |
 |
|
Иногда мне кажеться, что полиграфологи это особенные люди. Они умеют говорить, но не слышат то, что им говорят другие. Они умеют писать, но не читают то, что пишут другие.
_________________
http://skl-ol.ru
https://t.me/skl_ol |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Ср Мар 29, 2023 10:06 pm Заголовок сообщения: Добавлено: Ср Мар 29, 2023 10:06 pm Заголовок сообщения: |
 |
|
Что то писать и объяснять, что на форуме, что в виде статей видимо абсалютно бесполезно. Никто читать не будет, ни тем более разбираться...Вот интересно Комбинаторику Виленкина осилить - легко, а прочитать маленьки препринт и разобраться - .. не - а..ну... ни как...)
Пропробую запостить тогда картинки, что бы продемонстрировать полезность, которой...нет...
Вот САТ и бесполезность алгоритма, основанного на подсчёте числа комбинаций.

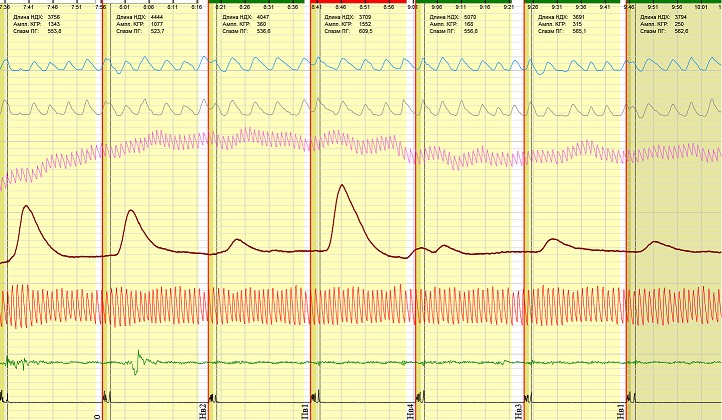
Вот первая версия, которая только лишь подсчитывает число комбинаций
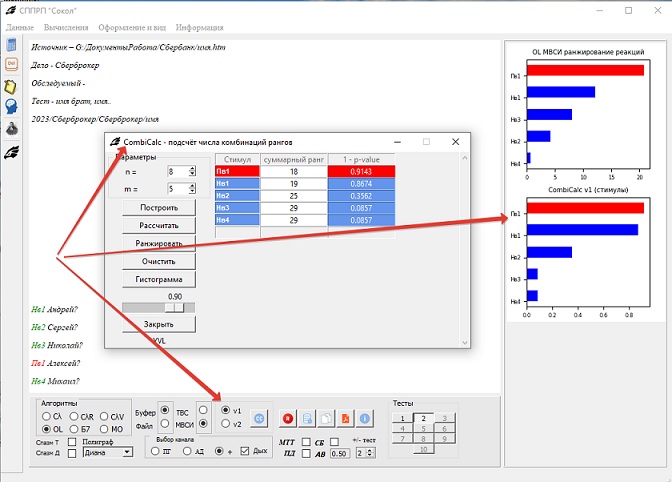
Но на основе подсчёта можно развить алгоритм так, что бы учитывался вес каждого канала и имелась возможность принимать решение на основе вычисления оценки вероятности
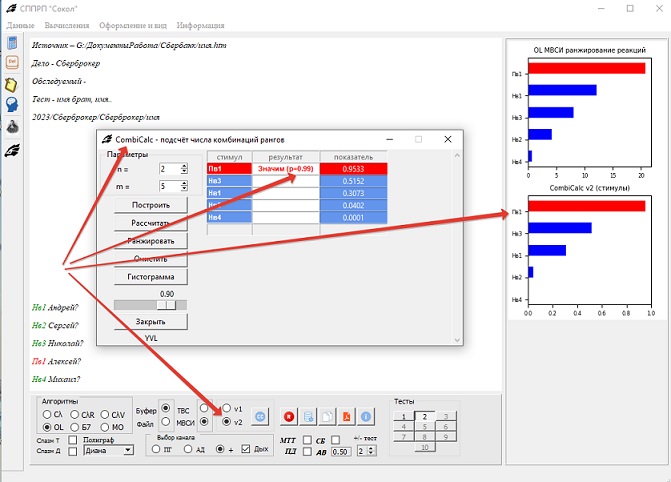
Можно сравнить с результатом другого алгоритма, котороый OL.
_________________
http://skl-ol.ru
https://t.me/skl_ol
Последний раз редактировалось: York (Ср Мар 29, 2023 11:04 pm), всего редактировалось 1 раз |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Ср Мар 29, 2023 10:13 pm Заголовок сообщения: Добавлено: Ср Мар 29, 2023 10:13 pm Заголовок сообщения: |
 |
|
Более того алгоритм подсчёта числа комбинаций можно использовать не только для рядов, но и для тестов вопросов сравнения. Правда благодаря простому подсчёту числа комбинаций можно толко построить гистограмку для наглядного восприятия. А вот если развить алгоритм, то можно научиться и решение принимать на основе вычисления вероятностей с использованием Байеса.
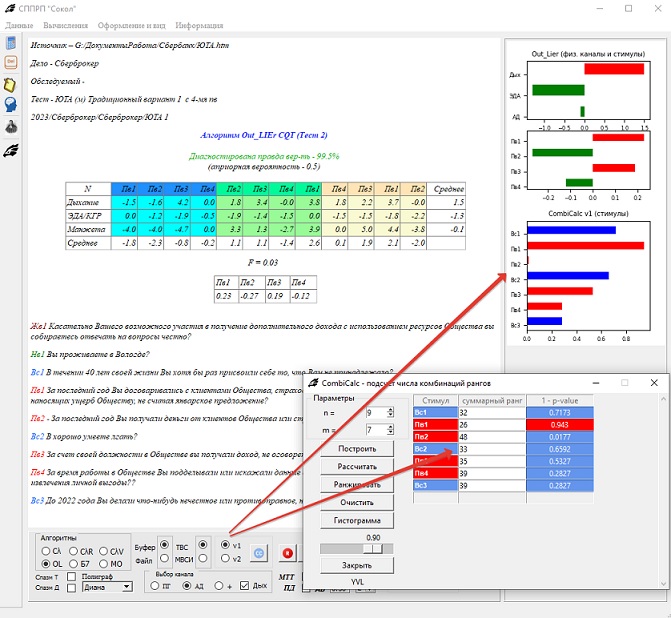
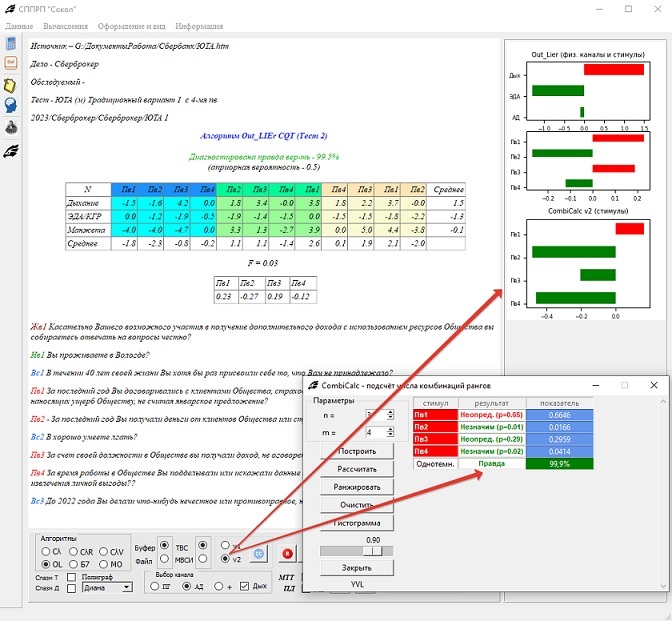
_________________
http://skl-ol.ru
https://t.me/skl_ol
Последний раз редактировалось: York (Ср Мар 29, 2023 10:19 pm), всего редактировалось 1 раз |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Ср Мар 29, 2023 10:16 pm Заголовок сообщения: Добавлено: Ср Мар 29, 2023 10:16 pm Заголовок сообщения: |
 |
|
А вот оценка точности алгоритма, основанного на подсчёте числа комбинаций, полученная на тестовой выборке (на выборке на которой алгоритм не обучался) Ч - чувствительность, С - специфичность, Т - общая точность
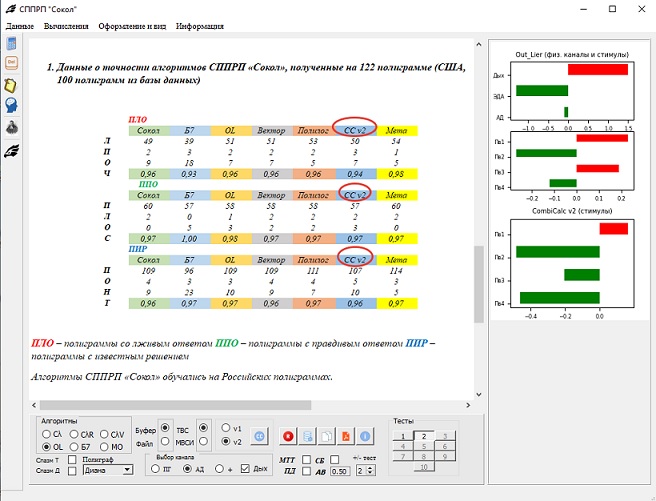
Что ещё сказать, или показать, что полезность у подсчёта числа комбинаций имеется вполне определённая, я уже и не знаю. Если нет желания увидеть, то и не будет видно...
_________________
http://skl-ol.ru
https://t.me/skl_ol |
|
| Вернуться к началу |
|
 |
$erP
Site Admin

Зарегистрирован: 29.06.2005
Сообщения: 7880
Откуда: Москва
|
 Добавлено: Ср Мар 29, 2023 11:11 pm Заголовок сообщения: Добавлено: Ср Мар 29, 2023 11:11 pm Заголовок сообщения: |
 |
|
| York писал(а): | | Вот интересно Комбинаторику Виленкина осилить - легко, а прочитать маленьки препринт - .. не - а..ну... ни как...) |
Голову чуть не сломал, но... осилил... осилил... )))
Желаете получить обратную связь... как-нибудь?

_________________
Мое почтение... $erP
................................... ЛЕГКО СОЛГАТЬ ТЯЖЕЛО |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Вс Апр 23, 2023 9:06 pm Заголовок сообщения: Добавлено: Вс Апр 23, 2023 9:06 pm Заголовок сообщения: |
 |
|
| $erP писал(а): |
Окончательная формула вычисления количества комбинаций дана на стр. 250.
|
Эта формула почти то, что нам надо, но чуть-чуть всё-таки не то.
А так ту формулу, что нужна легко получить не прибегая к использованию производящих функций. Её легко получить с помощью принципа включениё-исключений.
| $erP писал(а): |
Желаете получить обратную связь... как-нибудь?
|
Обратную связь всегда полезно получить. Правда сейчас появилась отличная от нуля возможность напечатать статью в рецензируемом журнале. Но переработнанную статью, поэтому и обратную связь по ней бы...
_________________
http://skl-ol.ru
https://t.me/skl_ol |
|
| Вернуться к началу |
|
 |
$erP
Site Admin

Зарегистрирован: 29.06.2005
Сообщения: 7880
Откуда: Москва
|
 Добавлено: Ср Апр 26, 2023 10:23 am Заголовок сообщения: Добавлено: Ср Апр 26, 2023 10:23 am Заголовок сообщения: |
 |
|
| York писал(а): | Эта формула почти то, что нам надо, но чуть-чуть всё-таки не то.
А так ту формулу, что нужна легко получить не прибегая к использованию производящих функций. Её легко получить с помощью принципа включениё-исключений. |
Там, по всей видимости, не одно, а несколько технических решений... Хотя они "взаимосвязаны"... Думал в сторону включений-исключений... но затем мозг пошел по пути самого наименьшего сопротивления...
| York писал(а): | | Обратную связь всегда полезно получить. Правда сейчас появилась отличная от нуля возможность напечатать статью в рецензируемом журнале. Но переработнанную статью, поэтому и обратную связь по ней бы... |
Да... без проблем... Только не очень быстро... сейчас есть свои задачи...
В какой форме нужна обратная связь?
_________________
Мое почтение... $erP
................................... ЛЕГКО СОЛГАТЬ ТЯЖЕЛО |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Ср Апр 26, 2023 11:25 am Заголовок сообщения: Добавлено: Ср Апр 26, 2023 11:25 am Заголовок сообщения: |
 |
|
Есть факты, которые вызывают удивление. Как оказалось меня ещё помнят преподаватели с кафедры прикладной математики Вологодского университета. Хотя тому уж тридцать лет, а какой-либо связи в любой форме не было. Короче пообещали дать статье направление от вуза в журнал. Хотя на данный момент это ещё не твёрдый факт, как я понимаю. Предполагается журнал "Математическое моделирование". Думаю будет в тему журнала, так как речь идёт о комбинаторной ранговой модели тестов МСИ. Нашёл на сайте журнала статью, котороя краешком, но касается полиграфа. Даже имеется слово "полиграфология" )
Математическая модель спонтанных реакций кожной проводимости человека
В статье выложу всю математику для МСИ, включая пресловутую формулу. Вообщем CombiCalc будут полностью открытым и исследованным алгоритмом, если статья состоится.
Сейчас подгоняю её под требования журнала. А обратную связь хотелось бы иметь в виде любых замечаний и т.д....А может в форме рецензии? Я тут опыта не имею...
Я думаю, если статья состоиться в таком солидном журнале, то это пойдёт на пользу полиграфу, а значит и всем полиграфологам. Для себя я какой-либо выгоды от статьи не вижу. Диссертацию защищать не собираюсь. Журнал математический, рецензенты математики с темой полиграфа незнакомые...И тут весомое слово от кандидата психолог. наук будет думаю не лишним.
_________________
http://skl-ol.ru
https://t.me/skl_ol |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Ср Апр 26, 2023 12:02 pm Заголовок сообщения: Добавлено: Ср Апр 26, 2023 12:02 pm Заголовок сообщения: |
 |
|
Сергей Владимирович, с другой стороны результаты статьи во многом основаны на Ваших данных, и на результатах Ваших исследований. В комбинаторике рангов тестов МСИ вы разобрались самостоятельно. Может быть в соавторы пойдёте? От этого статья только приобртёт. А Вам публикация может и пригодится...что б даром не пропадала...Может Вы ещё на докторскую пойдёте? )
_________________
http://skl-ol.ru
https://t.me/skl_ol |
|
| Вернуться к началу |
|
 |
$erP
Site Admin

Зарегистрирован: 29.06.2005
Сообщения: 7880
Откуда: Москва
|
 Добавлено: Ср Апр 26, 2023 2:13 pm Заголовок сообщения: Добавлено: Ср Апр 26, 2023 2:13 pm Заголовок сообщения: |
 |
|
Юрий Владимирович, спасибо за предложение... но нет.
При всём желании Вам как-то помочь, у меня сложилось отрицательное отношение к "формуле Ликкена" и основанных на этой формуле алгоритмов ЧансКалк и КомбиКалк (особенно версия 1). Это отношение обосновано как пониманием "изнутри" того, что делает "формула Ликкена", так и перепроверкой её эффективности на практическом материале: я перепроверил её работу на 100 тестах "виновных", 3 предъявления, 3 характеристики; 55 тестов "виновных", 4 предъявления, 3 характеристики; 45 тестов "невиновных", 3 предъявления, 3 характеристики... ничего хорошего, к сожалению, у меня не получилось...
В отношении обратной связи - давайте я опишу те "ляпы", которые я увидел в статье, и те сомнения, которые возникают в отношении правильности некоторых изложенных положений... Я уверен, что "ляпы" Вы и сами заметите, перечитав свою статью "с карандашом в руках"... а высказанные сомнения позволят подумать над тем, как, может быть, изложить некоторые положения более понятно или обоснованно... если это действительно покажется нужным.
В любом случае... четыре глаза лучше, чем два... и позволит повысить читабельность и качество Вашей статьи.
_________________
Мое почтение... $erP
................................... ЛЕГКО СОЛГАТЬ ТЯЖЕЛО |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Ср Апр 26, 2023 3:01 pm Заголовок сообщения: Добавлено: Ср Апр 26, 2023 3:01 pm Заголовок сообщения: |
 |
|
| $erP писал(а): |
При всём желании Вам как-то помочь, у меня сложилось отрицательное отношение к "формуле Ликкена" и основанных на этой формуле алгоритмов ЧансКалк и КомбиКалк (особенно версия 1). Это отношение обосновано как пониманием "изнутри" того, что делает "формула Ликкена", так и перепроверкой её эффективности на практическом материале: я перепроверил её работу на 100 тестах "виновных", 3 предъявления, 3 характеристики; 55 тестов "виновных", 4 предъявления, 3 характеристики; 45 тестов "невиновных", 3 предъявления, 3 характеристики... ничего хорошего, к сожалению, у меня не получилось...
|
По поводу КомбиКал v1 (а равно b ЧансКалк v1) я вообщем-то уже писал и не раз, что работает он не важно при использовании нескольких каналов. И особенно, что важно, плохо работает с поисковыми тестами. На уровне OSS(1,2) . В чём причина плохой работы с поисковыми я объяснял в статье. Более того это показано на примере численного моделирования. И подкреплено статистическими тестами.
А как он работает только с КГР, да ещё с десятью повторами, как вроде бы делал Ликкен, я не проверял. Хотя бы потому, что нет тестов в десять повторов. Хотя возможно он даст не плохие результаты. Можно прада покопаться в делах и подобрать дела где было нескольк ТЗВ и объеденить их и посмотреть.
СС v1 оставил в своей программе для целей виазуализации. Например ТВС он визиализирует очень даже неплохо. В дальнейшем если разработаю визуализацию результатов тестов на основе CC v2, то уберу СС v1 из программы.
А вот КомбиКал v2 показывает уже другие результаты. Гороздо лучшие чем v1. Не хуже чем имющиеся алгоритмы в OSS. В его основе лежит та же формула, но решение принимается с учётом весов физиологических показателей, которые вычисляются при обучении алгоритма.
Обучение алгоритма - это проблема. Проблема наличия валидных данных. СС v2 обучал на том, что было. На САТ-ах и на тестах с карточками. Не на тестах по уголовным делам. На этих тестах проверял СС v2. Результат хороший. Хотя если вычислить веса на тестах по уголовным делам то можно увидеть, что дыхание в тестах по уголовным телам играет более заметную роль чем в САТ-ах и карточках.
Но тем неменее даже при таком обучении алгоритм заработал неплохо.
Вообщем CombiCalc v2 это не застывшее г...), а живой организм, который может развиваться и обучаться. Были бы данные. Вот у Вас есть сто тестов...Поделитесь, а ?
ЧансКалк, который не v1 ... Я тут утверждать ничего не могу. Но уверен, что он то же как - то обучался и тоже использует веса каналов. Правда как обучался, какие веса я сказать не могу. Но его работу я проверял на тестах по уголовным делам. Работает. Не хуже чем алгоритмы в OSS. И наверняка может обучаться и дальше, и улучшать результаты.
| $erP писал(а): |
В отношении обратной связи - давайте я опишу те "ляпы", которые я увидел в статье, и те сомнения, которые возникают в отношении правильности некоторых изложенных положений... Я уверен, что "ляпы" Вы и сами заметите, перечитав свою статью "с карандашом в руках"... а высказанные сомнения позволят подумать над тем, как, может быть, изложить некоторые положения более понятно или обоснованно... если это действительно покажется нужным.
В любом случае... четыре глаза лучше, чем два... и позволит повысить читабельность и качество Вашей статьи. |
Да опишите, пожалуйста, ляпы. Препринту я не так много внимания уделил. Препринт есть препринт - можно переписывать не один раз. Это я так подумал с одной сторны. Для меня препринт в первую очередь это возможность записать то, что и как делал, что бы не забыть в дальнейшем окончательно. А при необходимости вспомнить. С другой стороны у меня сейчас стало заметно меньше времени заниматься всеми этими вещами, так как надо как то и на жизнь зарабатывать. То что четыре глаза лучше, чем два это абсолютно верно. Свой глаз конкретно замыливается и не видишь, что для другого как на ладони.
_________________
http://skl-ol.ru
https://t.me/skl_ol |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Ср Апр 26, 2023 4:48 pm Заголовок сообщения: Добавлено: Ср Апр 26, 2023 4:48 pm Заголовок сообщения: |
 |
|
Кстати, если говорить о том, ЧансКалк и КомбиКалк v1 имеют маленькую точность в работе с рядами, то надо сказать, чтто это самым прямым и непосредственным образом означает, что простое ранжирование реакций в ряду имеет низкую точность. Основа этих алгоритмов - ранжирование реакций. С помощью формулы алгоритмы всего лишь на основе суммарного ранга вычисляют некую универсальную меру для принятия решения. Универсальную в том смысле, что она одна для любого количества повторов теста и используемых физиологических каналов.
Знаю, что некоторые, а может и не только некоторые полиграфологи, используют ранжирование для оценки тестов. Так что вот ...имейте ввиду, что простое ранжирование - это процедура с низкой точностью.
_________________
http://skl-ol.ru
https://t.me/skl_ol |
|
| Вернуться к началу |
|
 |
York

Зарегистрирован: 29.09.2010
Сообщения: 2656
Откуда: Вологда
|
 Добавлено: Чт Апр 27, 2023 11:18 am Заголовок сообщения: Добавлено: Чт Апр 27, 2023 11:18 am Заголовок сообщения: |
 |
|
И справедливости ради, что бы у читателей не складывалось неверного впечатления от СС v1 добавлю, что ранжирование и формула очень хорошо работает в ТЗВ с непричастными
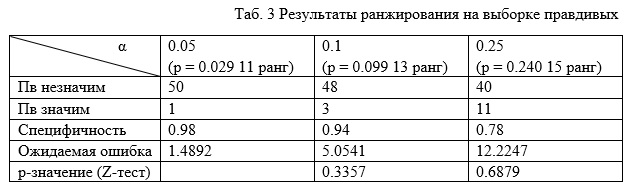
При альфа уровне 0.1 и выше даёт специфичность более 0.94. Это без неопределённых результатов.
И из таблицы видно, что ранговая модель, распределения вероятностей рангов расчитанные на её основе (по пресловутой формуле), очень хорошо соотвествуют ТЗВ с непричастными. Ожидаемая, расчитанная ошибка на основе модели, соотвествует ошибкам (Пв значим) полученным на тестах по реальным уголовным делам.
Проблема у такого способа классификации с чувствительностью.
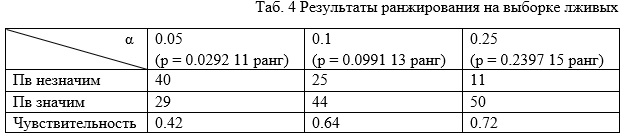
Если положить альфа уровен равным 0.25 (как рекомендуется в ЧенчКалк), то получаем более-менее сбалансированные показатели точности. Но довольно низкие: 0.72 и 0.78. Правда это без "нет решения" Если ввести такой исход, то возможно получились бы что-то более приемлимое. Подумалось: а чего я непопробовал? Наверное потому, что сразу занялся линейнык классифкатором.
А вот в случае поисковых тестов у СС v1, как ожидалось, ситуация похуже будет
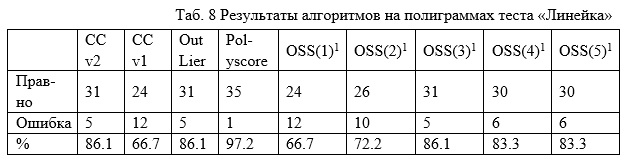
Только 67% правильных решений - 33% ошибок.
_________________
http://skl-ol.ru
https://t.me/skl_ol |
|
| Вернуться к началу |
|
 |
$erP
Site Admin

Зарегистрирован: 29.06.2005
Сообщения: 7880
Откуда: Москва
|
 Добавлено: Чт Апр 27, 2023 2:50 pm Заголовок сообщения: Добавлено: Чт Апр 27, 2023 2:50 pm Заголовок сообщения: |
 |
|
| York писал(а): | | Вот у Вас есть сто тестов...Поделитесь, а ? |
Да... конечно...
"Причешу" = удалю персональные данные... и скину...
_________________
Мое почтение... $erP
................................... ЛЕГКО СОЛГАТЬ ТЯЖЕЛО |
|
| Вернуться к началу |
|
 |
|
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
You cannot attach files in this forum
You cannot download files in this forum
|
Powered by phpBB © 2001, 2005 phpBB Group



|















